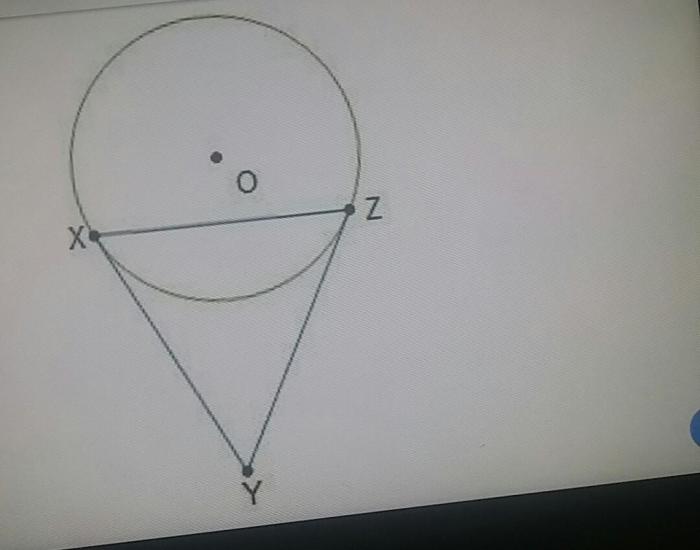
Line segments xy and zy are tangent to circle o – As line segments XY and ZY take center stage in their relationship with circle O, this exploration delves into the intriguing world of tangency. Tangency, a geometric concept that describes the unique interaction between lines and circles, unfolds here with clarity and precision, promising an enlightening journey into its properties, applications, and constructions.

The ensuing paragraphs unravel the intricate details of tangent line segments, their perpendicularity to radii at the point of tangency, and the constant product of their lengths. Real-world applications in geometry, engineering, and design showcase the practical significance of these concepts.

Methods for constructing tangent line segments to circles and proofs of key theorems further illuminate the subject matter, providing a comprehensive understanding of tangency and its implications.

Line Segments, Tangents, and Circles: Line Segments Xy And Zy Are Tangent To Circle O

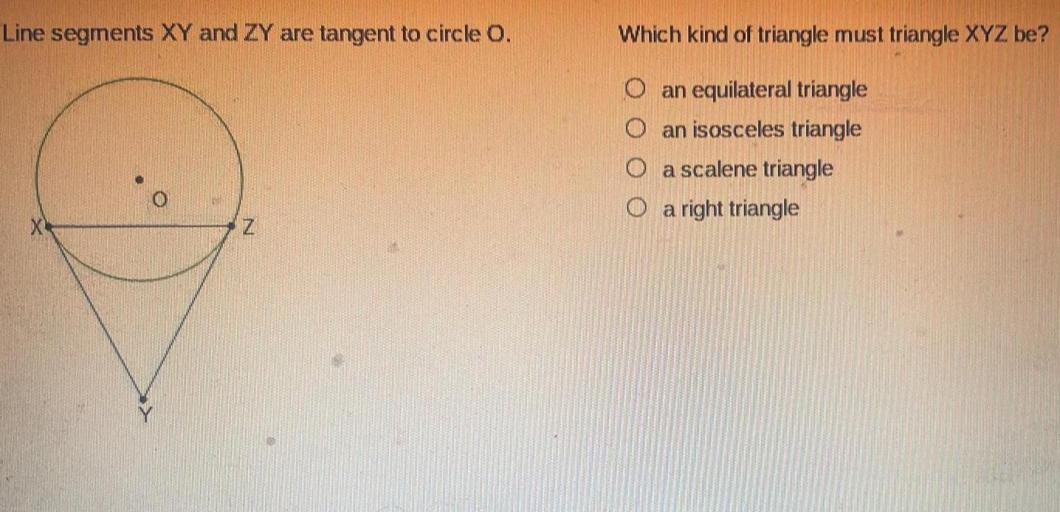
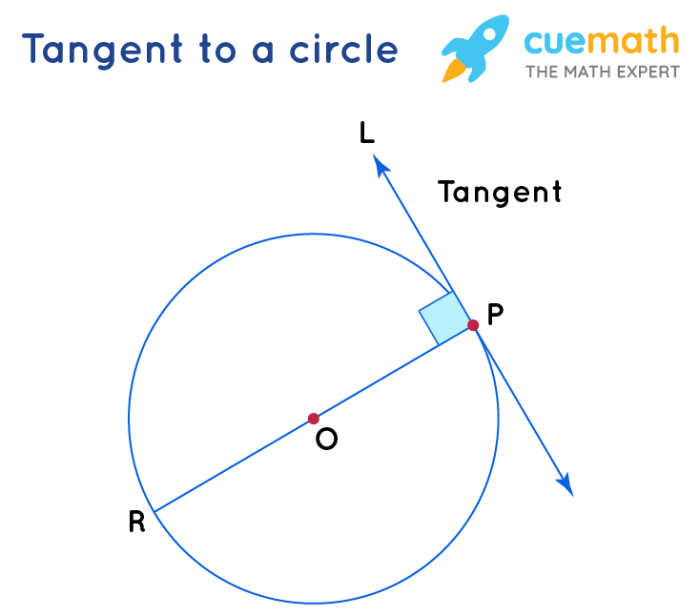
In geometry, a line segment is a straight path between two points. A tangent is a line that intersects a circle at exactly one point. A circle is a closed curve that lies in a plane and is equidistant from a fixed point, called the center.

Properties of Tangent Line Segments, Line segments xy and zy are tangent to circle o

Tangent line segments have several important properties. First, they are perpendicular to the radius of the circle at the point of tangency. Second, the length of a tangent line segment from an external point to a circle is equal to the square root of the difference between the square of the radius and the square of the distance from the external point to the center of the circle.

• Tangent line segments are perpendicular to the radius of the circle at the point of tangency.
• The length of a tangent line segment from an external point to a circle is equal to the square root of the difference between the square of the radius and the square of the distance from the external point to the center of the circle.

Applications of Tangent Line Segments

Tangent line segments have many applications in geometry, engineering, and design. For example, they can be used to construct circles, find the distance between two points, and determine the location of objects.

• Tangent line segments can be used to construct circles.
• Tangent line segments can be used to find the distance between two points.
• Tangent line segments can be used to determine the location of objects.

Constructions Involving Tangent Line Segments

There are several methods for constructing tangent line segments to a circle. One method is to use a compass and straightedge. Another method is to use a ruler and protractor.

• To construct a tangent line segment to a circle using a compass and straightedge:
  1. Draw a circle with center O and radius r.
  2. Choose a point P outside the circle.
  3. Draw a line segment from P to O.
  4. Construct the perpendicular bisector of PO.
  5. The perpendicular bisector of PO intersects the circle at two points, A and B.
  6. PA and PB are tangent line segments to the circle.
• To construct a tangent line segment to a circle using a ruler and protractor:
  1. Draw a circle with center O and radius r.
  2. Choose a point P outside the circle.
  3. Draw a line segment from P to O.
  4. Measure the angle between PO and the horizontal line.
  5. Construct an angle of the same measure at P, with PO as one side.
  6. The other side of the angle intersects the circle at point A.
  7. PA is a tangent line segment to the circle.

Proofs Related to Tangent Line Segments

There are several important theorems related to tangent line segments. One theorem states that the tangent line segment is perpendicular to the radius at the point of tangency. Another theorem states that the product of the lengths of the two tangent line segments from an external point to a circle is constant.

Theorem 1:The tangent line segment is perpendicular to the radius at the point of tangency.

Proof:Let O be the center of a circle, and let P be a point outside the circle. Let PA and PB be tangent line segments to the circle. Draw the radius OP. Since OP is a radius, it is perpendicular to the tangent line segment PA at point A.

Similarly, OP is perpendicular to the tangent line segment PB at point B. Therefore, the tangent line segment is perpendicular to the radius at the point of tangency.

Theorem 2:The product of the lengths of the two tangent line segments from an external point to a circle is constant.

Proof:Let O be the center of a circle, and let P be a point outside the circle. Let PA and PB be tangent line segments to the circle. Draw the radius OP. Since OP is perpendicular to PA and PB, it follows that the triangles OPA and OPB are right triangles.

Therefore, the product of the lengths of the two tangent line segments is equal to the product of the lengths of the two legs of the right triangle OPA, which is equal to the square of the radius of the circle.

Answers to Common Questions

What is the definition of a tangent line segment?

A tangent line segment is a line segment that intersects a circle at exactly one point, known as the point of tangency.

How do you prove that a line segment is tangent to a circle?

To prove that a line segment is tangent to a circle, you can show that it is perpendicular to the radius of the circle at the point of intersection.

What are some applications of tangent line segments?

Tangent line segments have applications in geometry, engineering, and design. For example, they can be used to construct circles, determine the location of objects, and design architectural structures.